Personally, I find vibration one of the most interesting phenomenons in the universe. It can be defined as a repetitive motion around an equilibrium point. It is one of the most important subjects that must be considered in engineering applications. Otherwise, you may face some undesirable outputs because of the excessive vibrations. Every
The simplest model of a vibrating system can be
Now, the simplest model of a vibrating system has become a mass-damper-spring model (Figure 1b) rather than a mass-spring model. This model reflects
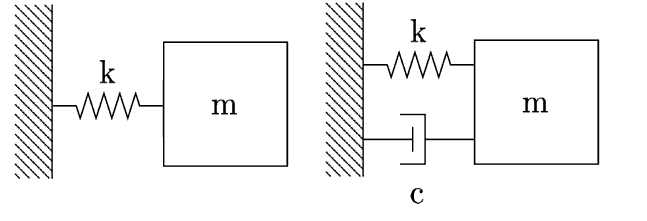
Figure 1- (a) a mass-spring model (b) a mass-damper-spring model
What it is written above may look straightforward but the problem is that the real engineering systems are not as simple as the simplest model. The simplest model that is defined here contains only one mass and this makes our system one degree of freedom. In other words, from this model, we can only obtain the motion in one direction. In reality, an object or an engineering product vibrates in every
Why is a vibration analysis needed? Which information can be obtained with this? It will be useful to consider our simplest model to answer this question. As we said earlier, each object/system vibrates and interestingly, it vibrates at a specific frequency. This means the number of oscillation in a second is always constant. The system wants to vibrate at that frequency, which is named natural frequency. It is interesting again that if the system is forced at its natural frequency, it vibrates with a larger amplitude. Generally, this larger amplitude is undesirable so we have to avoid this natural frequency of the system in order to get lower vibrations. This is for one degree of freedom systems (systems that are modelled with a mass) but the degree of freedom of a real system is infinite (in order to model a real system exactly, we need an infinite number of masses). Thus, we have an infinite number of natural frequencies for a real system and for each natural frequency, we have a vibration shape which is named mode shape (e.g. horizontal, vertical, torsional, bending etc.). Again, if the system is forced in the direction of its mode shape at that mode shape’s natural frequency, we will have larger amplitudes of vibration. Therefore, a vibration analysis gives us the frequencies and the directions which we have to avoid. If the system is forced at those directions and at those frequencies, the amplitude of the vibration will be very high (named resonance).
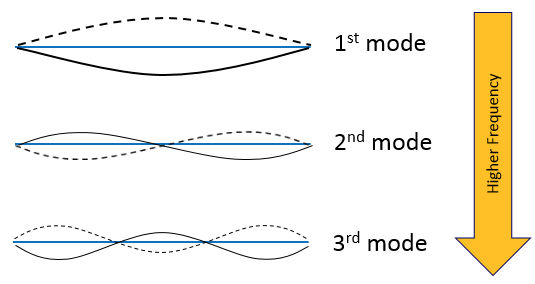
Different mode shapes for different natural frequencies of a cantilever beam
When someone who designs a system or a product knows those frequencies and those shapes, s/he can adjust them by changing the material and/or design according






Kayode Olonade
Really appreciated your expository skills and knowledge of vibrational resonance.