Sliding wear is one of the challenging engineering problems which often ends up with the ablation of contact materials. A number of experimental precedure exists to determine the total volume of wear debris produced. These methods ocassionally involved in laboratory condition sliding tests which are inevitably time consuming.
However, one theory named the Archard wear equation became very popular among scientists who were in search of understanding the wear problem. Therefore, in this post we will go into the details of famous “Archard Law” which is based on the theory of asperity contact.
Archard Law
Archard proposed this model before the contact mechanics laws were enunciated and was obtained from the model proposed by Holm [1], earlier. This model introduced a dimensionless coefficient ‘K’ to corroborate the experimental results with the proposed equations. Archard interpreted wear coefficient as a probability to form a wear particle by the contacting pair, although several authors interpret the wear coefficient differently.
When the material in sliding contact over each other, one or both will be exposed to wear with a height of h (mm) . Fig. 1 shows schematic of sliding wear of a block moving with the speed of v (mm/s) after sliding distance of s (mm).
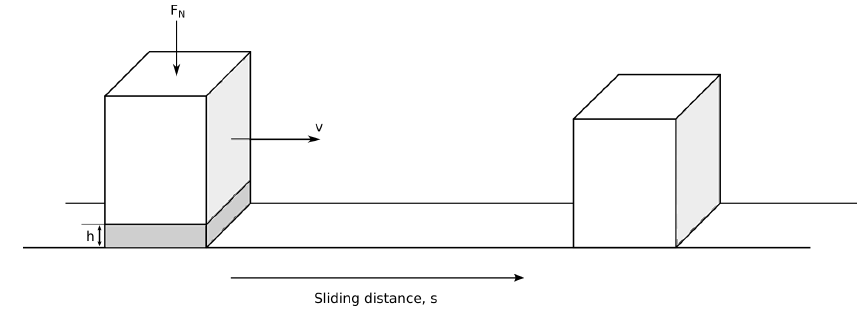
Under the perpendicular force of Fn (N) to the wear surface, the volume of material loss (Q) mm cubed can be calculated according to a theoretical approach proposed by Archard [52] as follows;
Q=\frac{K_{ad}.F_N.s}{H}If two materials in contact have different hardness values, H (MPa) is to be chosen that of the softer material. According to Archard’s law constant of Kad is named wear coefficient for adhesive wear.
References
1-H.C. Meng, K.C. Ludema, Wear, 181–183 (1995), pp. 443-457